PRIMTALL OG SAMMENSATTE TALL
Dersom du gjør om tallet 36 til et gangestykke, får du f.eks. ![]() . Kanskje tenkte du på
. Kanskje tenkte du på ![]() ,
, ![]() eller
eller ![]() istedenfor? Alle gangestykkene er riktige. Vi kaller tallet 36 et produkt. Tallene som multipliseres sammen kalles faktorer. De fleste tallene kan deles opp på denne måten, slike tall kalles sammensatte tall.
istedenfor? Alle gangestykkene er riktige. Vi kaller tallet 36 et produkt. Tallene som multipliseres sammen kalles faktorer. De fleste tallene kan deles opp på denne måten, slike tall kalles sammensatte tall.
Hvis du tenker deg om, vet du kanskje at det finnes tall du ikke kan dele opp på denne måten. Ta f.eks. tallet 13, det kan bare deles opp i ![]() . Det finnes ingen andre hele tall vi kan multiplisere og få 13 til svar. Tall som bare kan deles på seg selv og 1 kaller vi primtall. Her viser matematikken seg fra sin vakreste side, alle sammensatte tall kan deles opp i gangestykker som består av primtall. Det vil også hjelpe deg å forstå hvorfor det er fire ulike gangestykker som blir 36.
. Det finnes ingen andre hele tall vi kan multiplisere og få 13 til svar. Tall som bare kan deles på seg selv og 1 kaller vi primtall. Her viser matematikken seg fra sin vakreste side, alle sammensatte tall kan deles opp i gangestykker som består av primtall. Det vil også hjelpe deg å forstå hvorfor det er fire ulike gangestykker som blir 36.
PRIMTALLSFAKTORISERING
METODE 1
Dersom du er flink med multiplikasjon/divisjon, kan du starte med å dele opp et tall i et gangestykke. Deretter fortsetter du å dele opp tall i nye gangestykker helt til du bare sitter igjen med tall som ikke kan deles opp (primtall). Vi deler opp 36 i et gangestykke, det spiller ingen rolle hvordan du deler det opp. Deretter fortsetter vi å dele opp tallene i nye gangestykker (markert med gult). Tallene som ikke kan deles opp er markert med rødt. Uansett hvordan du starter å dele opp, vil du ende opp med at ![]() .
.
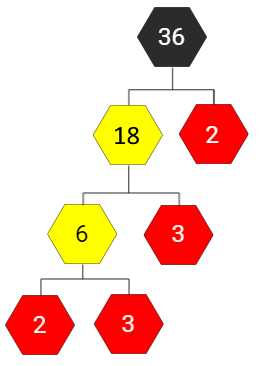 |
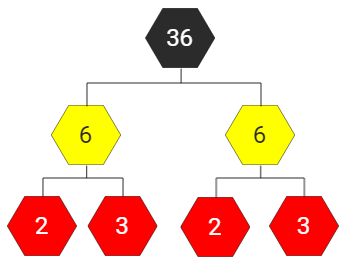 |
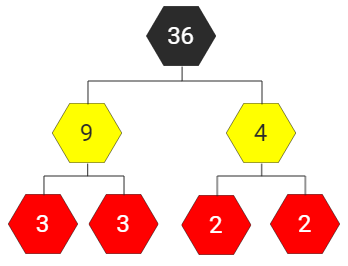 |
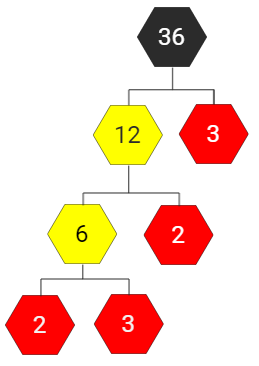 |
METODE 2
Du kan også lage deg en liste over primtallene som du bruker når du faktoriserer. De første primtallene er 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197 og 199.
Med denne metoden starter du alltid med det første primtallet, 2. Kan tallet divideres med 2? I så fall gjør du det. Fortsett med å spørre om svaret kan deles på 2. Når du ikke lenger kan dele på 2, går du videre til neste primtall. Kan tallet deles 3? For hver gang du svarer nei, hopper du videre til neste primtall.
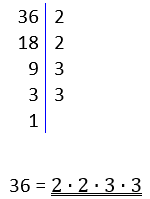 |
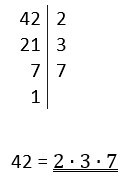 |
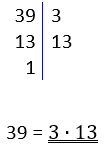 |
ANIMERT EKSEMPEL
 Du starter med å spørre om 48 kan deles på 2. Du skriver 2-tallet på høyre side av delestreken og skriver svaret 24 under 48. Deretter fortsetter du å spørre om 24 kan deles på 2. Vi skriver 2-tallet på høyre side av delestreken og 12 under 24. Kan 12 deles på 2? Ja. Da skriver du 2 til høyre for delestreken og 6 under 12. Legg merke til av enere står under enere, tiere under tiere osv. Deretter spør du om 6 kan deles på 2. Ja, da skriver du 2 til høyre for delestreken og 3 under 6. Du spør videre, kan 3 deles på 2? Nei. Da hopper du til neste primtall som er 3. Kan 3 deles på 3? Ja! Da skriver du 3 til høyre for delestreken og 1 under 3. Når svaret blir 1 er du ferdig med faktoriseringen. Skriv deretter opp tallet og faktorene i stigende rekkefølge.
Du starter med å spørre om 48 kan deles på 2. Du skriver 2-tallet på høyre side av delestreken og skriver svaret 24 under 48. Deretter fortsetter du å spørre om 24 kan deles på 2. Vi skriver 2-tallet på høyre side av delestreken og 12 under 24. Kan 12 deles på 2? Ja. Da skriver du 2 til høyre for delestreken og 6 under 12. Legg merke til av enere står under enere, tiere under tiere osv. Deretter spør du om 6 kan deles på 2. Ja, da skriver du 2 til høyre for delestreken og 3 under 6. Du spør videre, kan 3 deles på 2? Nei. Da hopper du til neste primtall som er 3. Kan 3 deles på 3? Ja! Da skriver du 3 til høyre for delestreken og 1 under 3. Når svaret blir 1 er du ferdig med faktoriseringen. Skriv deretter opp tallet og faktorene i stigende rekkefølge.

